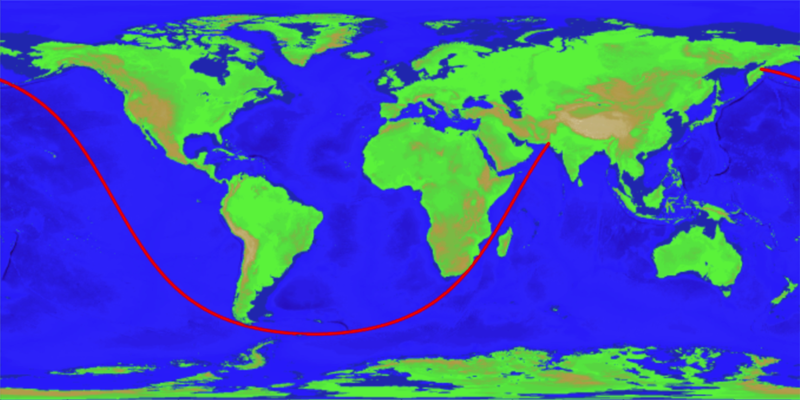
The longest sailable straight line path (shortest distance GC) on Earth.
Image: Chabukswar & Mukherjee, 2018
see also GCmap
Image: Chabukswar & Mukherjee, 2018
see also GCmap
From Gizmodo by George Dvorsky
Back in 2012, a Reddit user posted a map claiming to show the longest straight line that could be traversed across the ocean without hitting land.
Intrigued, a pair of computer scientists have developed an algorithm that corroborates the route, while also demonstrating the longest straight line that can be taken on land.
The researchers, Rohan Chabukswar from United Technologies Research Center Ireland, and Kushal Mukherjee from IBM Research India, created the algorithm in response to a map posted by reddit user user kepleronlyknows, who goes by Patrick Anderson in real life.
His map showed a long, 20,000 mile route extending from Pakistan through the southern tips of Africa and South America and finally ending in an epic trans-Pacific journey to Siberia.
On a traditional 2D map, the path looks nothing like a straight line; but remember, the Earth is a sphere.
Researchers confirm that the longest straight line
on Earth by sea without hitting land begins in Pakistan and ends at Russia.
on Earth by sea without hitting land begins in Pakistan and ends at Russia.
Rohan Chabukswar, Kushal Mukherjee | arXiv
Anderson didn’t provide any evidence for the map, or an explanation for how the route was calculated.
In light of this, Chabukswar and Mukherjee embarked upon a project to figure out if the straight line route was indeed the longest, and to see if it was possible for a computer algorithm to solve the problem, both for straight line passages on water without hitting land or an ice sheet, and for a continuous straight line passage on land without hitting a major body of water.
Their ensuing analysis was posted to the pre-print arXiv server earlier this month, and has yet to go through peer review.
One obvious way to calculate the straight lines would be through a so-called “brute force” method, requiring a computer to measure the length of every stretch of ocean.
To that end, Chabukswar and Mukherjee acquired a map from NOAA showing the Earth’s surface at a very reasonable resolution of one mile (1.8 km).
Anything above sea level was considered land, and everything below water—an obvious limitation, but it’s the best data the researchers could acquire.
More problematically, however, the high degree of resolution provided required a computer to parse through a mind-boggling number of routes.
“There would be 233,280,000 great circles to consider to find the global optimum, and each great circle would have 21,600 individual points to process—a staggering 5,038,848,000,000 points to verify,” the researchers wrote in their study.
Let’s read that number aloud for full impact: That’s five trillion, 38 billion, 848 million points.
Chabukswar and Mukherjee did not have the computing power for such an operation, nor the time, so they turned to an optimization scheme called “branch-and-bound.”
Computer scientists use branch-and-bound algorithms as a way to solve optimization problems, and it lowers the overall amount of search time by breaking up tasks into smaller chunks, or subsets.
The optimization happens as each subset is analyzed, and pruned when it doesn’t meet the search criteria.
As the branches and sub-branches are iteratively eliminated, so too is the amount of data that requires analysis.
Armed with this technique and a regular laptop computer, Chabukswar and Mukherjee calculated the sea route in just 10 minutes.
And fascinatingly, their algorithm came to the same answer as the one shown in Anderson’s map, showing a straight line that extends from Pakistan to Russia along a path that runs for 19,939 miles (32,089.7 km).
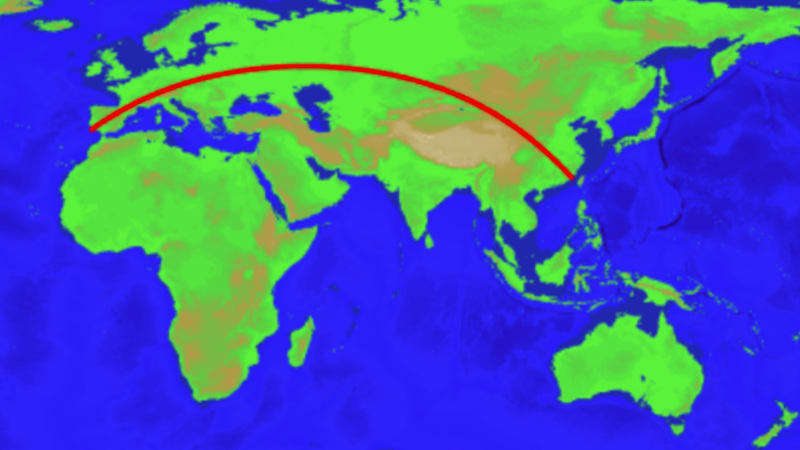
Longest driveable straight line path on Earth.
Image: Chabukswar & Mukherjee, 2018
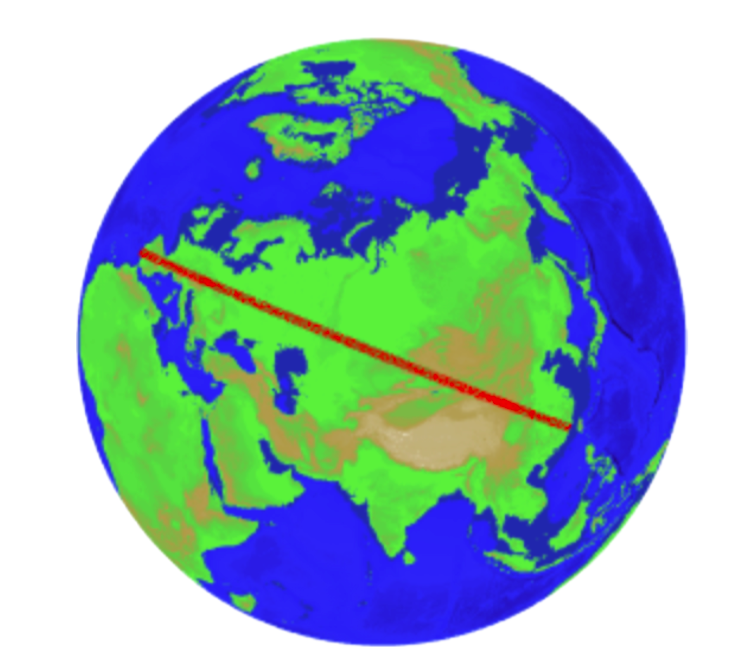
This view with a perspective directly above the path reveals a straight line.
Image: Chabukswar & Mukherjee, 2018
The researchers also calculated the longest possible straight line on land without hitting a major body of water, such as a lake.
The path, which took the computer 45 minutes to calculate, begins near Jinjiang, China, and cuts a swath through Mongolia, Kazakhstan and Russia.
The line continues through Poland, the Czech Republic, Germany, Austria, Liechtenstein, Switzerland, France, Spain, and finally ending near Sagres in Portugal.
That’s a total of 15 countries!
It’s not as long as the longest sailable path, but it still covers an impressive distance totaling 6,985 miles (11,241 km).
Chabukswar and Mukherjee call it a “driveable” path, but that’s highly unlikely given the many obstructions, such as mountains and forests, that are sure to be in the way.
Also, the land path intersects many rivers, which the researchers excluded as a variable.
Some major detours would likely be required to locate bridges, and to avoid some dangerous or challenging terrains.
On a similar note, the sea path, while a straight line, is probably not the safest or most ideal route given that it skirts treacherous Antarctic waters.
What’s more, the most expeditious sea route from Pakistan to Siberia would involve a trip through Indonesian waters, and the Philippine Sea.
As the researchers conclude in their study:
“The problem was approached as a purely mathematical exercise,” the researchers write.
“The authors do not recommend sailing or driving along the found paths.”
--------------------------------------------------------------------------------------------------------------------------
Comments from GeoGarage editor :
In the "Longest straight line paths on water or land on the Earth" document from Rohan Chabukswar and Kushal Mukherjee, the thrust of this paper is that they did a search of the possibilities to prove the original assertion, rather than just calculate it.
Their assumptions might also have been slightly different, given that they were using a dataset of heights with respect to sea level, rather than coastlines.
With the limits of the used dataset, the results show some issue in matter of lands crossing.
"The path originating in Sonmiani, Las Bela, Balochistan, Pakistan (25◦16′30′′ N, 66◦40′0′′), threading the needle between Africa and Madagascar, between Antarctica and Tiera del Fuego in South America (see above figures), and ending in Karaginsky District, Kamchatka Krai, Russia (58◦36′34′′ N, 162◦14′0′′ E)
The path covers an astounding total angular distance of 288◦35′23′′, for a distance of 32 089.7 kilometers.
The path covers an astounding total angular distance of 288◦35′23′′, for a distance of 32 089.7 kilometers.
This path is visually the same one as found by kepleronlyknows, thus proving his assertion"
In some previous articles from GeoGarage blog -see Links below- cited by the analysis, we also criticized the route given by kepleronlyknows, for the start and end points given the longest straight path you could travel on water without hitting land.
In practice, intermediate points along a Great Circle (GC) track are determined
and GC approximations are set by sailing a series of Rhumb Line (RL) tracks with constant courses.
View of the composite GC route (with 1731 wpts, length 10Nm)
on a Mercator map with OpenCPN software.
and GC approximations are set by sailing a series of Rhumb Line (RL) tracks with constant courses.
View of the composite GC route (with 1731 wpts, length 10Nm)
on a Mercator map with OpenCPN software.
So another Great Circle (GC) composite route -with the start and end positions provided by Rohan/Kushal- has been created in kmz format to be viewed in Google Earth with 1731 waypoints with different bearings separated by 10 Nm .
The total length of the GC route is 17316.5 Nm.
Start point (in red Rohan/Kushal)
End point (in red Rohan/Kushal)
by the way, the end point of the red route is 3.45 Nm inside the lands.
So the corrected length is 17,313 Nm
The issue is that :
the Red route (Rohan/Kushal) crosses 2 islands :
the Fenimore rock in the Aleutian Island chain (US Alaska), probably not on ETOPO1 shoreline...
 ... and also Anjouan island in the Comoros
... and also Anjouan island in the Comoros
(see yellow GE coastline)
the Fenimore rock in the Aleutian Island chain (US Alaska), probably not on ETOPO1 shoreline...
 ... and also Anjouan island in the Comoros
... and also Anjouan island in the Comoros(see yellow GE coastline)
see Rohan/Kushal route in Google Earth :
kmz file to open in GE
The path fits the brief—the longest continuous line across the earth’s waters—but you may want to think twice before firing up your rudderless boat.
Unfortunately, an autonomous boat probably won’t be sailing the newly verified path anytime soon.
In fact, the researchers don’t recommend that anyone sail or drive these paths since the algorithm analysis does not ensure safe conditions along these tracks.
Unfortunately, an autonomous boat probably won’t be sailing the newly verified path anytime soon.
In fact, the researchers don’t recommend that anyone sail or drive these paths since the algorithm analysis does not ensure safe conditions along these tracks.
The authors note, a little pointedly: “The problem was approached as a purely mathematical exercise." (ref : Ellipsoid model, geoid model or any other, see Figure of the Earth)
So the game to find the longest straight path you could travel on water without hitting land is still open...
So the game to find the longest straight path you could travel on water without hitting land is still open...
Links :
- ScienceMag : This ocean path will take you on the longest straight-line journey on Earth
- AtlasObscura : What is the longest straight line over water
- Outer Places : Researchers Say They've Found the Longest Straight Path by Sea on Earth
- Technology Review : Computer scientists have found the longest straight line you could sail without hitting land
- GeoGarage blog : The longest straight line you can sail on Earth ? / The 'Cooke passage' : a new world's longest straight-line sail ? / Sail all the way around the world to Antarctica without touching land in a straight line ? / What’s straight across the ocean when you’re at the beach






MapPorn : You can't travel in a straight line from Taiwan to the US West Coast without hitting land
ReplyDeleteMapPorn : You could sail in a straight line from Italy to Venezuela
ReplyDeleteBigThink : These are the world’s longest straight lines
ReplyDeleteYouTube : What's the Longest Straight Line You Can Sail Without Touching Land?
ReplyDeleteBigThink : The world’s longest straight line connects Portugal to China
ReplyDelete