Today March 5, 2012 marks the fitfth centenary of the birth of Gerardus Mercator who developed the famous map projection able to represent lines of constant course as straight segments, thus preserving the angles, which proved useful in navigation.
The 'Mercator projection' that bears his name was first used by him in 1569 for a wall map of the world on 18 separate sheets entitled:"New and more complete representation of the terrestrial globe properly adapted for its use in navigation."
The 'Mercator projection' had the property that lines of longitude, latitude and rhumb lines all appeared as straight lines on the map.
He had, he wrote on the map:
"... spread on a plane the surface of a sphere in such a way that the positions of all places shall correspond on all sides with each other both in so far as true direction and distance are concerned and as concerns true longitudes and latitudes."
With his world map published in 1569, the title of the original map telling us as much (Nova et aucta orbis terrae description ad usum navigantium emendate et accomodata translated as “new and improved description of the world amended and intended for the use of navigators”), the Flemish cartographer presented a new method to portray the globe on a two-dimensional, angle-preserving map.
This means that angles between the different directions on the map correspond to the directions on the earth’s surface.
On this Mercator projection, Greenland and South America appear similar in size.
The inset map shows that South America is actually about 15 times larger than Greenland.
(see "political controversy")
This means that angles between the different directions on the map correspond to the directions on the earth’s surface.
On this Mercator projection, Greenland and South America appear similar in size.The inset map shows that South America is actually about 15 times larger than Greenland.
(see "political controversy")
As it is impossible to project the spherical surface of the earth on a flat surface without distortion, Mercator’s cylindrical map projection uses these distortions to render them user-friendly for nautical purposes.
Although the Mercator projection significantly distorts scale and area (particularly near the poles), it has two important properties that outweigh the scale distortion:
- it’s a conformal projection, which means that it preserves the shape of relatively small objects. This is especially important when showing aerial imagery, because we want to avoid distorting the shape of buildings (square buildings should appear square, not rectangular).
- it’s a cylindrical projection, which means that north and south are always straight up and down, and west and east are always straight left and right.
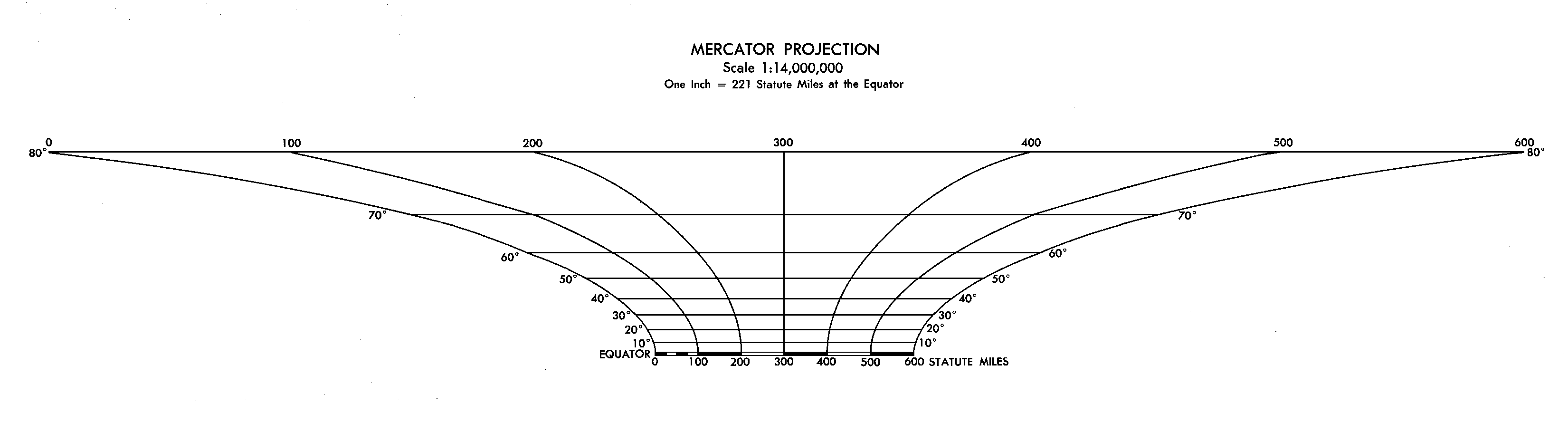
Graphic scale from a Mercator projection world map, showing the change with latitude -
A good illustration of how distorted the Mercator projection really is
(upload.wikimedia.org)
Google Maps is based on a close variant of the Mercator projection : to simplify the calculations, Google Maps uses the spherical form of this projection also called WGS84 web Mercator (or pseudo-Mercator), not the ellipsoidal form.Since the projection is mainly used for map display, and not for displaying numeric coordinates (the Latitude/Longitude geographic coordinates of features on Google Maps are the GPS coordinates based on the WGS 84 datum), we don’t need the extra precision of an ellipsoidal projection.
The difference between a sphere and the WGS 84 ellipsoid causes the resultant projection not to be precisely conformal.
However, the discrepancy is meaningless at the global scale but causes maps of local areas to deviate slightly from true ellipsoidal Mercator maps at the same scale.
However, the spherical projection causes approximately 0.33% scale distortion in the Y direction, which is not visually noticeable.
Since the Mercator projection goes to infinity at the poles, it doesn’t actually show the entire world : so Google Maps cannot show the poles.
Using a square aspect ratio for the map, the maximum latitude shown is approximately 85.05 degrees north and south.
Although cutting off coverage, this is not considered a limitation, given the purpose of the service for aid to navigation.
Not a lot of boats sail at those latitudes...
The great circle route from Seattle to London is a straight line on the gnomonic map projection.Circular “compass roses” at points where the route crosses major meridians are projected as ellipses, showing the distortion of directions that makes it possible to measure true azimuths only roughly along the route.
(courtesy of ESRI)
Portion of a world map made with the Mercator projection showing the rhumb line and great circle route from Seattle to London.The great circle route, obtained from a gnomonic projection, has been divided into 500 nautical mile legs.
Since the Mercator projection is conformal, each simplified compass rose is correctly projected as a circle.
(courtesy of ESRI)
Originally designed for use in nautical navigation, Mercator's projection is a map of the Earth's surface on which straight lines, called rhumb lines (or loxodromes), represent a course of constant compass heading.
On the surface of a sphere, however, such rhumb lines are not the shortest distance between two points. Rather, the shortest distance between two points is a great circle (or orthodromes), whose shape is displayed for the routes on the Marine GeoGarage charts (great circle distance calculations)
Links :
- Wikipedia : History of cartography
- University of Chicago : Rhumb lines and map wars, a social history of the Mercator (by Mark Monmonier)
Mercator Puzzle, great way to see the heinous distortion that Mercator has unleashed on the world
ReplyDeleteThe Guardian : Why Google Maps gets Africa wrong
ReplyDeleteDailyMail : Why every world map you're looking at is WRONG: Africa, China and India are distorted despite access to accurate satellite data
ReplyDeleteInteractive map tool shows the true size of the world's countries
ReplyDelete